Il Decision tree è un albero decisionale, un algoritmo impiegato per offrire supporto al processo di decision-making.
Serve a pianificare azioni in grado di sostenere i decisori aziendali in azienda. Ecco quale ruolo ricopre nel data mining.
Cos’è un Decision tree
A Decision tree è un algoritmo di apprendimento supervisionato non basato su parametri, usato per affrontare attività di classificazione o di regressione. Utilizza il grafo ad albero in cui i nodi interni (nodi foglie) si caratterizzano per offrire nuovi input.
Utilizza una struttura gerarchica ad albero, organizzata attraverso un nodo radice, rami, nodi interni e nodi foglia.
Gli archi che derivano dai nodi etichettati con una caratteristica sono catalogati con ognuno dei possibili valori della peculiarità stessa. Ogni foglia dell’albero è etichettata con una classe o una probabilità di distribuzione sulle classi.
L’apprendimento da un albero avviene dividendo la fonte sottoinsiemi sulla base di un test di attribuzione di valore. Si reitera questo processo su ogni sottoinsieme derivato, seguendo un modello ricorsivo noto come partizionamento ricorsivo o recursive partitioning.
La ricorsività è completata quando il sottoinsieme a un nodo raggiunge tutti gli stessi valori di una variabile target, o quando la divisione non aggiunge più valori alle previsioni.
Questo processo di induzione top-down del Decision tree è un esempio di Greedy algorithm, un algoritmo che segue l’euristica di problem-solving, grazie alla scelta ottimale locale in ogni fase. Rappresenta la più comune strategia di alberi decisionali di apprendimento.
Consente di classificare le istanze di big data. Nella struttura ad albero i nodi foglia costituiscono le classificazioni e le ramificazioni il set delle proprietà che conducono a quelle classificazioni. Dunque ciascun nodo interno è una macro-classe frutto dell’unione delle classi riferite ai suoi nodi figli.
Il Decision tree nel data mining si suddivide in due tipologie:
- l’albero di classificazione: quando la risposta è una variabile nominale, per esempio se un email è spam o no;
- Regression tree: il risultato previsto rientra invece nei numeri reali (per esempio: il salario di un lavoratore).
Elementi dell’albero di decisione
Gli elementi del Decision tree sono i nodi, compreso il nodo radice e quello foglia, l’arco, la foglia e il cammino. Ecco come sono legati insieme.
Ciascun nodo interno costituisce una variabile. L’arco verso un nodo figlio funge da valore riferito a quella proprietà. Una foglia rappresenta il valore relativo alla variabile obiettivo, partendo dai valori delle altre proprietà. Nell’albero le altre proprietà si riferiscono al cammino (path) dal nodo radice (root) al nodo foglia.

Parametri di split e pruning
Di solito si costruisce un albero di decisione attraverso tecniche di apprendimento basate sull’insieme dei dati iniziali (dataset), suddiviso in due sottoinsiemi: il training set su cui si costruisce la struttura dell’albero; il test set che permette di sottoporre a test l’accuratezza del modello predittivo così realizzato.
A ciascun nodo interno, su cui avviene la ripartizione dei dati, è legato a un predicato detto condizione o parametro di split.
In molte scenari occorre definire un parametro di arresto (halting) o anche parametro di potatura (pruning), per stabilirne la massima profondità.
L’aumento della profondità di un albero ovvero della sua dimensione non ha un impatto diretto sull’efficacia del modello. Infatti, un incremento eccessivo della profondità dell’albero potrebbe causare una crescita sproporzionata della complessità computazionale rispetto ai vantaggi in merito all’accuratezza delle classificazioni e previsioni.
I parametri più diffusioni per le condizioni di split sono l’indice di Gini (Gini index), impiegato da Cart (Classification and Regression Trees), il tasso d’errore nella classificazione (misclassification error) e la variazione di entropia (entropy deviance).
L’indice di Gini e la variazione di entropia sono i criteri che indirizzano la realizzazione dell’albero. Invece la valutazione del tasso di errore nella classificazione permette di ottimizzare l’albero attraverso il processo di pruning (“potatura” dei nodi superflui).
In un albero di decisione ben fatto, i nodi foglia dovrebbero includere solo istanze di dati associati ad una sola classe. Un’ottimizzazione dell’albero cercare di minimizzare il livello di entropia via via che dalla radice si procede verso le foglie. Dunque, la valutazione dell’entropia stabilisce, fra le varie possibilità disponibili, quali sono i parametri di split migliori per l’albero di classificazione.

Overfitting
Gli alberi decisionali complessi hanno la tendenza all’overfitting, dunque non si riescono a generalizzare efficacemente con i nuovi dati. I processi di pre-potatura o post-potatura permettono di evitare questo scenario. La pre-potatura interrompe la crescita degli alberi quando ci scarseggiano i dati. Invece la post-potatura, dopo la creazione dell’albero, rimuove gli alberi secondari contenenti dati inadeguati.
Regole di decisione
L’albero decisionale parte con un nodo radice senza rami in entrata. Ad alimentare i nodi interni, quelli decisionali, sono i rami in uscita dal nodo radice. Entrambi i nodi permettono di effettuare valutazioni per creare sottoinsiemi omogenei, rappresentati da nodi foglia o nodi terminali, sulla base delle funzionalità a disposizione. I nodi foglia costituiscono il ventaglio di tutti i possibili risultati nell’ambito del dataset.
Per prendere le decisioni è possibile impiegare le regole decisionali, creando una struttura del diagramma di flusso. La rappresentazione del processo decisionale è semplice da interpretare e consente a più gruppi appartenenti ad un’organizzazione di capire bene il motivo per cui è stata presa una decisione. Nella figura Ibm propone un esempio in cui si decide se andare a fare surf o no.
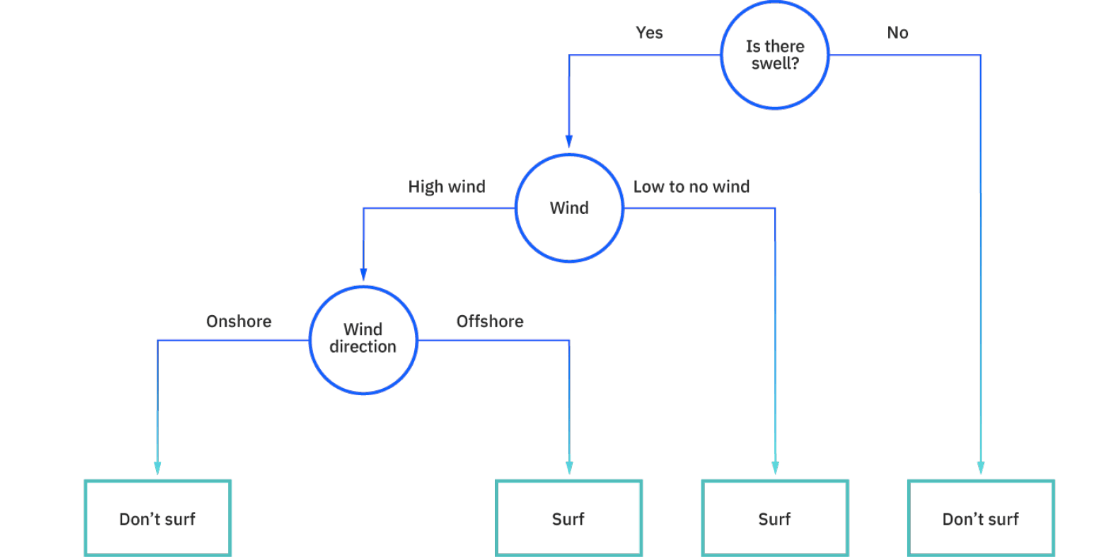
La teoria delle decisioni
Nella teoria delle decisioni, che valuta la decisione più conveniente fra quelle possibili, secondo metodi matematico-statistici, prende in esame le conseguenze frutto di ogni decisione presa.
A iniziare dall’insieme delle decisioni possibili, da quello degli stati di natura esterni a chi prende le decisioni e da una quantificazione delle conseguenze (funzione di perdita), una decisione si considera più conveniente ovvero preferibile quando la perdita che ne deriva è inferiore.
L’economista e matematico A. Wald (1902-1950) formulò la teoria delle decisioni nel 1939, ricollegandosi alla teoria dei giochi di J.L. von Neumann del 1928, sotto il profilo di taluni aspetti formali. Ma nella teoria dei giochi, tuttavia, sono presenti più player in gioco.
Il modello decisionale è un modello logico-matematico di un problema di decisioni, in cui i dati del problema sono l’espressione quantitativa di ciò che definisce il problema, le variabili di decisione descrivono le scelte possibili da parete del decisore, i vincoli del problema rappresentano i rapporti fra le scelte e la funzione utilità (o funzione costo od obiettivo) costituisce una o più funzioni di valutazione delle possibili scelte. I modelli di ottimizzazione fanno parte dei modelli decisionali.
Tipologie di alberi decisionali
L’algoritmo introdotto da Hunt degli anni ’60 ha permesso di modellare l’apprendimento umano in psicologia. Rappresenta la base dei più diffusi algoritmi dell’albero decisionale: ID3, C4.5, CART.
Ross Quinlan ha contribuito a sviluppare Iterative Dichotomiser 3 (ID3). L’algoritmo utilizza l’entropia e il guadagno di informazioni come metriche per verificare e “pesare” le divisioni dei candidati.
L’algoritmo C4.5 è un’iterazione successiva di ID3, elaborato sempre da Quinlan. Può sfruttare il guadagno di informazioni o i rapporti di guadagno per prendere in esame e “pesare” i punti di divisione all’interno degli alberi decisionali.
I Classification and regression tree (CART) sono alberi di classificazione e regressione di Leo Breiman. L’algoritmo sfrutta il metodo delle impurità di Gini per valutare l’attributo su cui operare la divisione. Le impurità di Gini servono a calcolare la frequenza con cui un attributo, frutto di una scelta a caso, è erroneamente classificato. La valutazione che utilizza l’impurità Gini punta ad ottenere un valore più basso possibile.
I benefici
Gli alberi decisionali trovano impiego in un’ampia gamma di casi, anche se ci sono altri algoritmi che forniscono performance superiori rispetto agli algoritmi dei Decision tree. Tuttavia, l’utilità degli alberi decisionali emerge proprio nelle attività di knowledge discovery e data mining.
I vantaggi che offrono sono evidenti: sono semplici e immediati da interpretare, grazie alla logica booleana e alle rappresentazioni visive; riducono la preparazione dei dati e si possono inoltre gestire valori anche in assenza di alcuni valori; sono flessibili sia in termini di classificazione che in fase di regressione; infine non sono sensibili alle relazioni fra gli attributi, il che vuol dire che se esiste un’elevata correlazione fra due variabili, l’algoritmo può sceglierne solo una per eseguire la suddivisione.
Problemi con più uscite
I decision tree sono metodi semplici, ma presentano alcuni problemi. Una problematica è l’elevata varianza nei modelli risultanti che l’albero decisionale produce.
Per mitigare questo problema, sono stati sviluppati metodi d’insieme di Decision tree. In particolare, esistono due ensemble method attualmente molto diffusi: gli alberi decisionali allenati con il metodo di bagging e quelli con il metodo di boosting.
Gli alberi decisionali allenati con il metodo di bagging (ovvero media delle stime) si basano su un metodo per minimizzare la varianza degli alberi di decisionali. Permettono di costruire decision tree multipli reiterando i resampling training data con la sostituzione e votando gli alberi di decisioni con la consensus prediction. Questo algoritmo è noto come Random forest: la tecnica della foresta casuale è un’evoluzione del Decision tree.
Gli alberi decisionali allenati con il metodo di boosting. Il gradiente di boosting combina apprendimenti deboli. In questo caso, il Decision tree in un singolo apprendimento forte, adatta un albero debole ai dati ed iterativamente continua l’adattamento degli apprendimenti deboli al fine di correggere l’errore del precedente modello.






