Un Box Plot è un grafico statistico dalle molteplici potenzialità, in grado di fornire uno strumento utile al Data analyst per svolgere il proprio lavoro.
Il grafico “box and whiskers plot”, in italiano si traduce come “diagramma a scatola e baffi”. Sono anche noti come Box Plot degli outlier o dei quantili.
I grafici hanno il vantaggio, rispetto a una media e a una deviazione standard, di descrivere la forma di ogni tipo di variabile quantitativa, anche in presenza in outliers e asimmetrie pronunciate.
I grafici a scatola sono tra i grafici più comuni, insieme ai popolari istogrammi, per rappresentare in maniera grafica le variabili quantitative. Consentono di esporre rapidamente un’idea della distribuzione della variabile e valutarne l’andamento. In presenza di dati molto contenuti, se le variabili fossero nominali o categoriche, converrebbe utilizzare un grafico a barre.
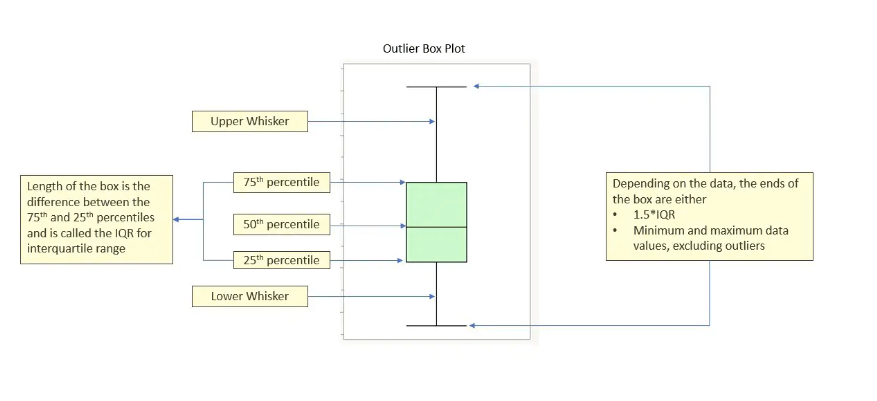
Cos’è e cosa si intende per Box Plot
Un Box Plot è una rappresentazione di una distribuzione: è un grafico statistico che illustra la distribuzione dei dati nel caso di una variabile continua.
Aiuta a visualizzare il centro e la distribuzione dei dati, fungendo da strumento visivo per verificare la normalità o individuare possibili outlier, dal momento che permette di comprendere la simmetria di una distribuzione o meno.
Dunque consente di mettere a confronto la forma di più distribuzioni. Ma soprattutto mette il Data scientist nelle condizioni di individuare in modo veloce e puntuale valori anomali e outliers. Infatti, il professionista dei dati è colui che vanta le competenze per analizzare e aggregare i dati, per studiare, per esempio, l’andamento di un prodotto sul mercato, fornendo, così, alla sua azienda i tool per sviluppare i propri modelli di business in maniera lungimirante, guadagnando in competitività.
Nel dettaglio, il Box Plot consente di rappresentare sul medesimo grafico, cinque tra le misure riferite alla posizione più comuni in statistica.
Rispetto agli istogrammi, i grafici più comuni, il Box Plot non presenta alcune peculiarità della distribuzione come picchi o valli. Dunque, non consente di comprendere se una distribuzione sia bi-modale (ovvero con due picchi distinti) e non dice se è presente un “buco” fra le osservazioni.
Ma il Box Plot è più adatto dell’istogramma quando occorre identificare eventuali valori anomali. Inoltre, la semplicità del Box Plot lo rende preferibile soprattutto per campioni di piccole dimensioni, nel caso si vogliano confrontare graficamente più distribuzioni.
Come creare, costruire e usare un Box Plot
Innanzitutto, la struttura del Box Plot è una sintesi a cinque numeri appartenenti a una variabile quantitativa.
Sono infatti cinque indici di una variabile:
- il valore minimo (Q0);
- il primo quartile (25esimo percentile oQ1);
- la mediana (Q2 o 50esimo percentile o Q2);
- il terzo quartile (75esimo percentile o Q3);
- il valore massimo (Q4).
Per generare un Box Plot si calcola:
- la mediana, il 25° e il 75° percentile;
- il range interquartile (IQR) come differenza tra il 75° e il 25° percentile;
- la lunghezza massima dei baffi moltiplicando l’IQR per 1,5;
si individuano gli outlier; si utilizzano le statistiche calcolate in questo modo, per immettere i risultati in un Box Plot.
Il grafico “box and whiskers plot” (in italiano: “diagramma a scatola e baffi”) è una scatola (appunto, il box) tra il primo e terzo quartile.
Essa presenta l’ampiezza della metà centrale della distribuzione. L’altezza della scatola, infatti, coincide col range interquartile (IQR): contiene il 50% centrale delle osservazioni svolte, quelle che si trovano fra il primo e il terzo quartile.
La mediana è inoltre la linea dentro la scatola.
I due segmenti che dalla scatola si prolungano verso l’alto e verso il basso sono i cosiddetti “baffi”. Esprimono la dispersione dei valori sotto il primo quartile e sopra il terzo quartile, quelli non etichettati come outliers.
Il valore superiore fra quelli presenti nella variabile che non individua un’anomalia, costituisce il termine del baffo superiore. Analogamente, il valore inferiore, escluse le anomalie, delimita la fine del baffo inferiore.
In presenza di valori anomali, questi ultimi apparirebbero nel Box Plot come punti isolati o al di sopra e/o al di sotto dei baffi della distribuzione.
Dunque, la scatola definisce e consente di comprendere cosa accade al 50% dei valori osservati. Inoltre, i baffi accendono un faro sulle code della distribuzione, mentre i punti isolati rappresentano in generale gli eventuali outliers.

Come si interpreta un Box Plot
Per poter interpretare correttamente un Box Plot, è necessario osservare qual è la scala di misura della variabile in esame. A indicarla è l’asse verticale delle ordinate ovvero l’asse y.
Dopo aver verificato la scala numerica, bisogna focalizzarsi sulla linea della mediana, perché si tratta del valore centrale della distribuzione. Dunque, occorre guardare la dispersione, notando sia quanto la scatola è alta sia quanto i baffi sono lunghi.
Distribuzione dei dati
Il baffo superiore va verso l’alto fino al valore massimo che è inferiore o uguale di 3/2 volte il range interquartile (IQR). Il baffo inferiore invece si estende verso il basso fino al più piccolo valore che sia maggiore o uguale a 3/2 (ovvero 1,5) volte il range interquartile.
I valori che si distanziano dal box di più di 3/2 volte IQR verso l’alto o il basso (ovvero fuoriescono dai baffi) costituiscono potenziali outliers e sono indicati con punti.
Box Plot ed Excel: qual è il collegamento
Il collegamento fra Box Plot ed Excel è evidente perché si usa il foglio di calcolo, per calcolare la mediana e gli altri elementi necessari per disegnare la scatola.
Su Excel, bisogna selezionare i dati (anche impiegando una o più serie di dati), quindi si va sulla barra multifunzione, digitando sulla scheda Inserisci e poi su Icona Grafico statistiche, scegliendo scatola e baffi.
Facendo clic su una delle caselle del grafico, è possibile selezionare la casella, e dunque digitare su formato sulla barra multifunzione. Utilizzando gli strumenti della scheda formato barra multifunzione, è infine possibile modificare a piacere.

La relazione fra gli outliers con i Box Plot
Uno degli elementi che confonde l’interpretazione del Box Plot riguarda gli estremi dei baffi in presenza di outliers.
Ma basta ripercorrere la genesi del Box Plot, per chiarirsi le idee in proposito.
Mary Eleanor Spear espose nel 1952 una prima versione del grafico a scatola. E lo battezzò range-bar. Questo grafico era così composto: una parte centrale era il box, mentre due segmenti laterali si estendevano da una parte fino al valore minimo e dall’altra fino a quello massimo.
In questa prima release, gli estremi dei baffi cadevano sempre insieme coi valori estremi della distribuzione. Coincidevano con loro. Tuttavia questa versione rischiava di essere fuorviante in presenza di outliers, che estendevano alquanto le lunghezze dei baffi.
Per superare questo ostacolo, nel 1970 lo statistico americano John Tukey rielaborò il range-bar per ideare il suo erede, il Box Plot. Un grafico grafico in grado di descrivere la distribuzione dei dati e al contempo di identificare i potenziali outliers.
Per focalizzare la scoperta dei valori anomali, Tukey stabilì soglie (in inglese: fences) in grado di isolare gli outliers:
- la soglia inferiore è in Q1-1,5*IQR
- quella superiore in Q3 + 1,5*IQR-
Dunque, basta moltiplicare per 1,5 l’altezza della scatola, per riportare questo range al di sopra del terzo quartile ed al di sotto del primo quartile. I valori che fuoriescono da tale range sono gli outliers.
Infatti, in caso di presenza di valori anomali, gli estremi dei baffi del Box Plot non rappresentano il valore minimo e massimo della variabile, bensì coincidono con i valori più estremi inferiori ai Tukey fences, ovvero alle soglie fissate.
Esempi di Box Plot
Sono numerosi gli esempi di Box Plot. Ne riportiamo solo alcuni fra i più comuni:
- possono essere usati nell’agro-alimentare per calcolare le calorie, una variabile continua, in una porzione di food da vendere al supermercato;
- in statistica, per confrontare i voti degli esami in presenza rispetto ai voti in DAD;
- per rappresentare il numero di automobili che passano in un’area nell’arco di un anno;
- nell’ambito della finanza e dell’economia.




